This is my first year teaching any algebra higher than Algebra I, so my first year teaching factoring sums/differences of cubes. Naturally, I jumped right in teaching my students the same methodology I have always used. Two formulas. One for sums. One for differences. Same, opposite, positive. See below our INB notes from earlier this school year. It was all well and good until we encountered the problem -216(u^2)+(u^5).
It is unique because the first term is negative. So, we had to consider the sign of that term but not the sign of the second term since it is built into the formula. Students naturally had questions, and I explained that the formula accounts for the sign of the second term since we choose the formula based on the addition or subtraction. But we have to manually adjust for the sign of the first term. Which caused me to think, for the first time in my life, why teach two formulas? If there are some cases were we have to remember the cube root is negative, why not just do that for all cases? So, when we recently encountered this lesson in Algebraic Connections, I decided to give it a spin. See below.
Also, drawing on my experience the first time around, I decided to have students make a list of each power of a and b before plugging in the formula. The combination of these two things made this lesson go much more smoothly, and that was with a group of students who don't love math. ;) Both times around, I had my students include the page below in their notebooks as a reference, which was really useful. I have always found that my students especially benefit from making a list of perfect squares and cubes of variables since those don't follow the same intuition as constants.
A fun aside: Some of my advanced students wanted to know if there was a quick way to generate this list in their calculators, and then they worked together to come up with the idea of entering x squared and x cubed in the y= menu and then looking at the table to get the list. I love that kind of curiosity and problem-solving!
Download:
Factoring Sum or Difference of Cubes
Perfect Squares and Cubes
Download:
Factoring Sum or Difference of Cubes
Perfect Squares and Cubes

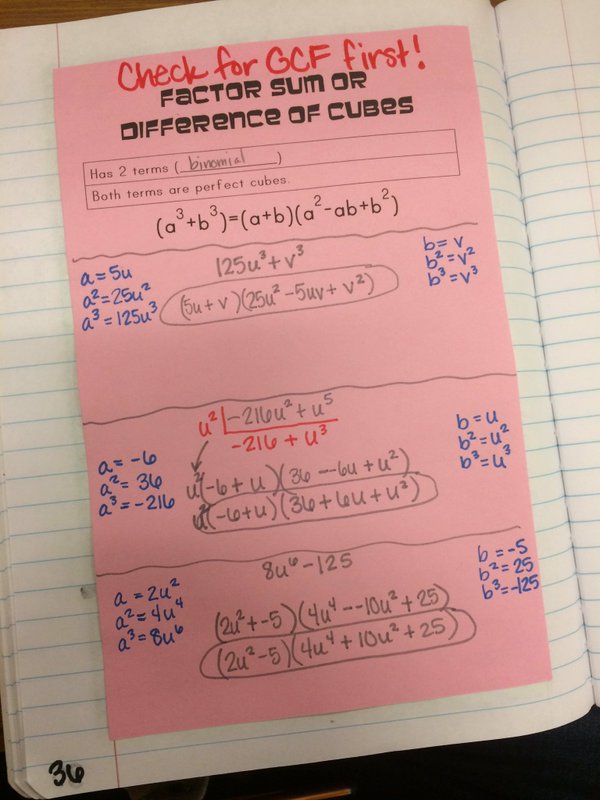


 RSS Feed
RSS Feed
